纤维范畴
在讨论所谓的纤维范畴前,我们先了解什么是强笛卡尔态射。
令$p : \mathcal{S} \to \mathcal{C}$为一个$\mathcal{C}$上的范畴。给定一个对象$x \in \mathcal{S}$其满足$p(x) = U$,并且给定一个态射$f : V \to U$,我们可以尝试取某种“纤维积$V \times _ U x$”(或者一个$x$通过$V \to U$的基变换)。换句话说,一个从对象$z \in \mathcal{S}$打到$V \times _ U x$的态射应该由一个有序对$(\varphi , g)$给定,其中$\varphi : z \to x$,$g : p(z) \to V$使得$p(\varphi ) = f \circ g$。图像上看,
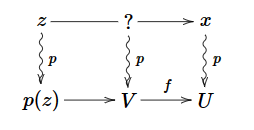
如果这样一个态射$V \times _ U x \to x$存在,那么它被叫做一个强笛卡尔态射。
令$\mathcal{C}$为一个范畴,$p : \mathcal{S} \to \mathcal{C}$为一个$\mathcal{C}$上的范畴。
一个强笛卡尔态射,或更准确的,一个强$\mathcal{C}$-笛卡尔态射是一个$\mathcal{S}$的态射$\varphi : y \to x$,使得对每个$z \in \mathop{\mathrm{Ob}}\nolimits (\mathcal{S})$映射 $$\mathop{\mathrm{Mor}}\nolimits _\mathcal {S}(z, y) \longrightarrow \mathop{\mathrm{Mor}}\nolimits _\mathcal {S}(z, x) \times _{\mathop{\mathrm{Mor}}\nolimits _\mathcal {C}(p(z), p(x))} \mathop{\mathrm{Mor}}\nolimits _\mathcal {C}(p(z), p(y)),$$
其由$\psi \longmapsto (\varphi \circ \psi , p(\psi ))$给定,是双射的。
我们称$\mathcal{S}$是一个$\mathcal{C}$上的纤维范畴,如果给定任意一个打到$U \in \mathop{\mathrm{Ob}}\nolimits (\mathcal{C})$上的$x \in \mathop{\mathrm{Ob}}\nolimits (\mathcal{S})$与任意一个$\mathcal{C}$中的态射$f : V \to U$,都存在一个打到$f$上的强笛卡尔态射$f^*x \to x$。
Related
There is currently no relevant content for this entry