Almost-mathematics is a tool studying $p$-adic Hodge theory. In this section, we use the book of Gabber and Ramero, [20], as our main reference like Peter Scholze in [16].

Unless otherwise stated, all rings are commutative with identity. We fixed a base ring $V$ that contains an ideal $\mathfrak{m}$ satisfying $\mathfrak{m}^{2} = \mathfrak{m}$. And we also assume that $\widetilde{\mathfrak{m}} := \mathfrak{m}\otimes_{V}\mathfrak{m}$ is a flat $V$-module. For the definition of tensor product, see §11.

Question 3.1. Let $(V,\left| \cdot \right|)$ be a non-discrete valuation ring of rank 1, and $\mathfrak{m}$ is an ideal of $V$. If we have $\mathfrak{m}^{2} = \mathfrak{m}$, can we get that $\mathfrak{m}$ is the maximal ideal of $V$?

The basic idea of almost-mathematics is that one neglects $\mathfrak{m}$-torsion everywhere.

Definition 3.2. Let $M$ be a $V$-module. We say that $M$ is almost zero if $\mathfrak{m}M$ = 0. A map of $V$-modules $\phi: M\rightarrow N$ is an almost isomorphism, if Ker $\phi$ and Coker $\phi$ are both almost zero $V$-modules. Then we say that $M$ is almost isomorphic to $N$.

Remark 3.3. A map of $V$-modules $\phi: M\rightarrow N$ is almost injective if $\textrm{Ker }\phi$ is almost zero. And $\phi$ is almost surjective if $\textrm{Coker }\phi$ is almost zero.

Proposition 3.4. A $V$-module $M$ is almost zero if and only if $\mathfrak{m}\otimes_{V} M = 0$.

Proof. Just consider the natural isomorphism $V\otimes_{V}M\cong M$.

Proposition 3.5. A map $\varphi:M\rightarrow N$ of $V$-modules is an almost isomorphism if and only if the induced map $\widetilde{\mathfrak{m}}\otimes_{V}M\rightarrow \widetilde{\mathfrak{m}}\otimes_{V}N$ is an isomorphism.

Proof. First we assume that $\varphi:M\rightarrow N$ is almost isomorphic. Consider the exact sequence $$ \textrm{Ker }\varphi\rightarrow M\rightarrow N\rightarrow \textrm{Coker }\varphi; $$

since $\widetilde{\mathfrak{m}}$ is flat, we have the induced exact sequence $$ \widetilde{\mathfrak{m}}\otimes_{V}\textrm{Ker }\varphi\rightarrow \widetilde{\mathfrak{m}}\otimes_{V}M\rightarrow\widetilde{\mathfrak{m}}\otimes_{V}N\rightarrow\widetilde{\mathfrak{m}}\otimes_{V}\textrm{Coker }\varphi. $$

Since Ker $\phi$ and Coker $\phi$ are both almost zero $V$-modules, we have the following exact sequence $$ 0\rightarrow \widetilde{\mathfrak{m}}\otimes_{V}M\rightarrow\widetilde{\mathfrak{m}}\otimes_{V}N\rightarrow0, $$

which implies that $\widetilde{\mathfrak{m}}\otimes_{V}M\rightarrow\widetilde{\mathfrak{m}}\otimes_{V}N$ is an isomorphism.

Conversely, assume that $\widetilde{\mathfrak{m}}\otimes_{V}M\rightarrow\widetilde{\mathfrak{m}}\otimes_{V}N$ is an isomorphism. We consider the exact sequence again $$ \textrm{Ker }\varphi\rightarrow M\rightarrow N\rightarrow \textrm{Coker }\varphi. $$

Then similarly, we have the induced exact sequence $$ \widetilde{\mathfrak{m}}\otimes_{V}\textrm{Ker }\varphi\rightarrow \widetilde{\mathfrak{m}}\otimes_{V}M\rightarrow\widetilde{\mathfrak{m}}\otimes_{V}N\rightarrow\widetilde{\mathfrak{m}}\otimes_{V}\textrm{Coker }\varphi.$$

Since $\widetilde{\mathfrak{m}}\otimes_{V}M\rightarrow\widetilde{\mathfrak{m}}\otimes_{V}N$ is an isomorphism, we conclude that $\widetilde{\mathfrak{m}}\otimes_{V}\textrm{Ker }\varphi=\widetilde{\mathfrak{m}}\otimes_{V}\textrm{Coker }\varphi=0$. So we get $\mathfrak{m}\otimes_{V}\textrm{Ker }\varphi=\mathfrak{m}\otimes_{V}\textrm{CoKer }\varphi=0$ as desired.

Lemma 3.6. If $\mathfrak{m}$ is flat, then we have an isomorphism $\widetilde{\mathfrak{m}}\cong\mathfrak{m}$ of $V$-modules.

Example 3.7. If $V$ is a non-discrete valuation ring of rank one, then its maximal ideal $\mathfrak{m}$ is flat as a $V$-module by ([11], Tag0539). Therefore, we have $\widetilde{\mathfrak{m}}\cong\mathfrak{m}$.

Proposition 3.8. The set of all almost isomorphisms forms a multiplicative system.

Proof. First, any identity of $V$-module is almost isomorphic. And the composition of almost isomorphic maps is almost isomorphic. Given a map of $V$-modules $g:X\rightarrow Y$, an almost isomorphic map of $V$-modules $t: X\rightarrow Z$, and a $V$-module $W$. Then we have an induced solid diagram

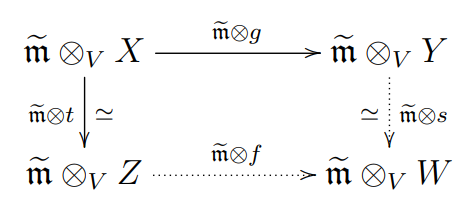
which is made to be commutative with $\widetilde{\mathfrak{m}}\otimes s:\widetilde{\mathfrak{m}}\otimes_{V}Y\cong \widetilde{\mathfrak{m}}\otimes_{V}W$ and $\widetilde{\mathfrak{m}}\otimes f:\widetilde{\mathfrak{m}}\otimes_{V}Z\rightarrow\widetilde{\mathfrak{m}}\otimes_{V}W$. So the solid diagram

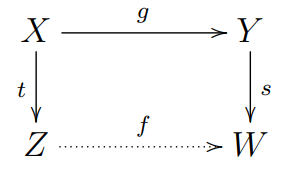
can be made to be commutative with a map of $V$-modules $f: Z\rightarrow W$ and an almost isomorphic map of $V$-modules $s: Y\rightarrow W$.

Given a pair of maps of $V$-modules $f,g: X\rightarrow Y$ and an almost isomorphic map of $V$-modules $t: Z\rightarrow X$ such that $f\circ t=g\circ t$. We have the induced maps $f',g':\widetilde{\mathfrak{m}}\otimes_{V}X\rightarrow\widetilde{\mathfrak{m}}\otimes_{V}Y, t':\widetilde{\mathfrak{m}}\otimes_{V}Z\cong\widetilde{\mathfrak{m}}\otimes_{V}X$ such that $f'\circ t'=g'\circ t'$. Then there exists an almost isomorphic map of $V$-modules $s: Y\rightarrow I$ such that $s':\widetilde{\mathfrak{m}}\otimes_{V}Y\cong\widetilde{\mathfrak{m}}\otimes_{V}I$ satisfies $s'\circ f'=s'\circ g'$ by virtue of $f'\circ t'=g'\circ t'$. Consequently, we have $s\circ f=s\circ g$.

We have just proved the left multiplicative case. However, the right multiplicative case is similar.