Complex Analytic Spaces

Published at 2024-07-11 11:53:57Viewed 177 times
未经作者授权，请勿转载

In this section, we will introduce the so-called complex analytic spaces using ([46]) as our reference.

Definition 4.1. Let $K$ be a ring. A $K$-locally ringed space is a locally ringed space $(X,\mathscr{O}_{X})$ equipped with a $K$-algebra structure $p$ in $\mathscr{O}_{X}$. A $K$-algebra structure $p$ in $\mathscr{O}_{X}$ is a collection of ring homomorphisms $p_{U}:K\rightarrow\mathscr{O}_{X}(U)$, one for each open $U\subset X$, such that for every $U_{1}\supset U_{2}$ the following diagram commutes:

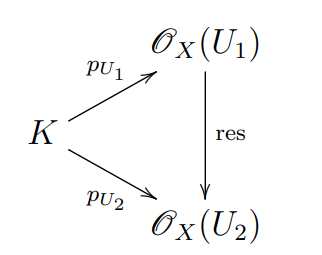
If $z\in\mathscr{O}_{X}(U)$ and $a\in K$, we usually write $az$ instead of $p_{U}(a)z$.

Let $(X',\mathscr{O}_{X'})$ be another $K$-locally ringed space. A morphism of $K$-locally ringed space or simply a $K$-morphism from $(X,\mathscr{O}_{X})$ to $(X',\mathscr{O}_{X'})$ is a morphism $(f,f^{*})$ of locally ringed spaces such that $$ f^{*}_{U'}\circ p'_{U'}=p_{f^{-1}(U')} $$ for every open set $U'\subset X'$.

Example 4.2. The complex number space $$ \mathbb{C}^{n}=\{(\xi_{1},...,\xi_{n})\mid\xi_{i}\in\mathbb{C}\textrm{ for }1\leq i\leq n\}$$ will be viewed as a $\mathbb{C}$-locally ringed space with the natural structure as follows:

The underlying topological space is $\mathbb{C}^{n}$ equipped with the standard topology. And the structure sheaf $\mathscr{O}_{\mathbb{C}^{n}}$ is the sheaf of homological functions. Namely, for each open set $U\subset\mathbb{C}^{n}$, $\mathscr{O}_{\mathbb{C}^{n}}(U)$ is the $\mathbb{C}$-algebra of all holomorphic functions on $U$, where the elements of $\mathbb{C}$ are identified with constant functions. Moreover, any open subset $V$ of $\mathbb{C}^{n}$ will be also viewed as a $\mathbb{C}$-locally ringed space with the structure sheaf $\mathscr{O}_{V}$ obtained as the restriction of $\mathscr{O}_{\mathbb{C}^{n}}$ to $V$.

Example 4.3. Let $V$ be an open subset in $\mathbb{C}^{n}$ and let $(h_{1},...,h_{m})$ be a finite system of holomorphic functions in $V$. Let $$S=\{\xi\in V\mid h_{i}(\xi)=0,1\leq i\leq m\},$$ with the induced topology from $\mathbb{C}^{n}$. The quotient sheaf of $\mathscr{O}_{V}$ by the ideal generated by $(h_{1},...,h_{m})$ is concentrated on $S$. We will denote by $\mathscr{O}_{S}$ the restriction of this sheaf to $S$. Then we obtain a $\mathbb{C}$-locally ringed space $(S,\mathscr{O}_{S})$ with the $\mathbb{C}$-algebra structure $\rho$ which is the identification of constants with constant functions.

Definition 4.4. A complex analytic space or simply a $\mathbb{C}$-space is a locally ringed space $(X,\mathscr{O}_{X})$ such that every point in $X$ admits an open neighborhood $U$ such that $(U,\mathscr{O}_{X|U})$ is $\mathbb{C}$-isomorphic to some $(S,\mathscr{O}_{S})$ described in Example 4.3.

References

  1. [1]HH. Matsumura, Commutative Ring Theory. Vol. 8 of Cambridge Studies in Advanced Mathematics(1989).
  2. [2]N. Bourbaki, Éléments de mathématique. Fasc. XXX. Algébre commutative. Chapitre 6: Valuations. Actualités Scientifiques et Industrielles, No. 1308. Hermann, Paris, 1964.
  3. [3]N. Bourbaki, Algebra II, Chapters 4-7, Elements Of Mathematics, Springer, Berlin, Heidelberg, 2003.
  4. [4]Pierre Antoine Grillet, Abstract Algebra, 2nd ed., Graduate Texts in Mathematics, vol. 242, Springer-Verlag New York, 2007.
  5. [5]Serge Lang, Algebra, 3nd ed., Graduate Texts in Mathematics, vol. 211, Springer-Verlag New York, 2002.
  6. [6]Serge Lang, Algebraic Number Theory, 2nd ed., Graduate Texts in Mathematics, vol. 110, Springer, New York, NY, 1994.
  7. [7]Siegfried Bosch, Lectures on formal and rigid geometry, volume 2105 of Lecture Notes in Mathematics. Springer, Cham, 2014.
  8. [8]S. Bosch, U. Güntzer, and R. Remmert, Non-Archimedean analysis. A systematic approach to rigid analytic geometry, Grundlehren der mathematischen Wissenschaften 261, Springer-Verlag Berlin, Heidelberg 1984.
  9. [9]Linus Kramer, Locally Compact Groups and Lie Groups, Part I Basic Properties of Topological Groups, 1 Topological Groups, https://www.uni-muenster.de/AGKramer/content/ch1.pdf, 2020.
  10. [10]Tammo Tom Dieck, Algebraic Topology, European Mathematical Society, Chapter 1 Topological Spaces, 1.7 Topological Groups, 2008.
  11. [11]Stack Project authors, Stack Project, https://stacks.math.columbia.edu/, 2022.
  12. [12]Dinakar Ramakrishnan and Robert J. Valenza, Fourier analysis on number fields, Graduate Texts in Mathematics, vol. 186, Springer-Verlag, New York, 1999.
  13. [13]Pierre Deligne, Cohomologie Étale, Séminaire de Géométrie Algébrique du Bois-Marie SGA 4 1/2, Springer-Verlag Berlin Heidelberg, Lecture Notes in Mathematics, volume 569, 1977.
  14. [14]Alexander Grothendieck and Michèle Raynaud, Revêtements Étales et Groupe Fondamental, Lecture Notes in Mathematics, Volume 224, Springer, Berlin, Heidelberg, 1971.
  15. [15]Alexander Grothendieck, Artin, M. and Verdier, J. L. Théorie des Topos et Cohomologie Étale des Schémas. Séminaire de Géométrie Algébrique du Bois-Marie 1963-1964 (SGA 4), Springer-Verlag Berlin Heidelberg, 1973.
  16. [16]Peter Scholze, Perfectoid Spaces, IHES Publ. math. 116 (2012), pp. 245-313.
  17. [17]Peter Scholze, Étale cohomology of diamonds, Preprint, 2018.
  18. [18]R. Huber. Continuous valuations. Math. Z., 212(3):455-477, 1993.
  19. [19]Bjorn Poonen, Rational Points on Varieties, Graduate Studies in Mathematics, Volume 186, American Mathematical Society, 2017.
  20. [20]O. Gabber and L. Ramero. Almost ring theory, volume 1800 of Lecture Notes in Mathematics. Springer-Verlag, Berlin, 2003.
  21. [21]Ofer Gabber and Lorenzo Ramero, Foundations For Almost Ring Theory, Release 7.5, 2019.
  22. [22]Jean-Marc Fontaine and Yi Ouyang, Theory of p-adic Galois Representations, preprint, 2008.
  23. [23]James Dugundji, Topology, Allyn and Bacon, Inc.470 Atlantic Avenue, Boston., 1966.
  24. [24]Antoine Ducros, Charles Favre and Johannes Nicaise, Berkovich Spaces and Applications, Springer International Publishing, Lecture Notes in Mathematics, Volume 2119, 2015.
  25. [25]Vladimir G. Berkovich, Spectral Theory and Analytic Geometry over Non-Archimedean Fields, American Mathematical Society, 1990.
  26. [26]Vladimir G. Berkovich, Étale cohomology for non-Archimedean analytic spaces, Publications Mathématiques de l'Institut des Hautes Études Scientifiques 78, 5-161 (1993). https://doi.org/10.1007/BF02712916.
  27. [27]Peter J. Hilton and Urs Stammbach, A Course in Homological Algebra, Graduate Texts in Mathematics, Volume 4, Springer-Verlag New York, 1997.
  28. [28]A. Grothendieck and J. A. Dieudonné, Eléments de Géométrie Algébrique I, Springer-Verlag Berlin Heidelberg New York, 1971.
  29. [29]A. Grothendieck, Some aspects of homological algebra, https://www.math.mcgill.ca/barr/papers/gk.pdf, 2011.
  30. [30]Neal Koblitz, Introduction to Elliptic Curves and Modular Forms, 2nd ed., Graduate Texts in Mathematics, Volume 97, Springer-Verlag New York, Inc., 1993.
  31. [31]Fred Diamond and Jerry Shurman, A First Course in Modular Forms, Graduate Texts in Mathematics, Volume 228, Springer-Verlag New York, 2005.
  32. [32]Neal Koblitz, p-adic Numbers, p-adic Analysis, and Zeta-Functions, Graduate Texts in Mathematics, Volume 58, Springer, New York, NY, 1984.
  33. [33]Fernando Q. Gouvêa, p-adic Numbers An Introduction, 3rd ed, Universitext, Springer, Cham, 2020.
  34. [34]J-P. Serre, A Course in Arithmetic, Graduate Texts in Mathematics, Volume 7, Springer, New York, NY, 1973.
  35. [35]J-P. Serre, Local Fields, Graduate Texts in Mathematics, Volume 67, Springer, New York, NY, 1979.
  36. [36]Jean-Pierre Serre, Galois Cohomology, Springer-Verlag Berlin Heidelberg, 1997.
  37. [37]Tim Browning and Florian Bouyer, Local Fields, Bouyer, https://warwick.ac.uk/fac/sci/maths/people/staff/fbouyer/local_fieldstcc.pdf, 2013.
  38. [38]Paul J. McCarthy, Algebraic extensions of fields, New York: Dover Publications., 1991.
Get connected with us on social networks! Twitter

©2024 Guangzhou Sinephony Technology Co., Ltd All Rights Reserved