·

Why infinite sum need to be made sense ?

Published at 2024-10-25 18:15:49Viewed 71 times

Academic article

·

Note

Please reprint with source link

Writing categories

Abstract algebra

Differential geometry

My question: For example, the sum in the partition of unity,

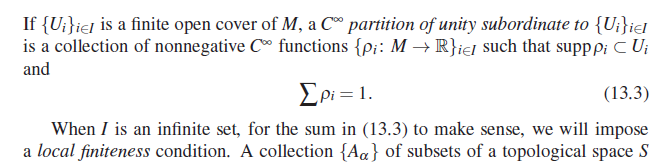
and the polynomial expression in abstract algebra.

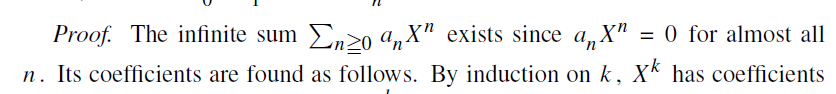
Answer: Sums with an infinite number of terms (or "series" in more formal terms) need some extra conditions to make sure they are "well behaved". Otherwise you can get paradoxes like the following:

$$\begin{align} &S = 1 + 1 + 1 + \dots \\ &\Rightarrow 2S = 2 + 2 + 2 + \dots \\ &\Rightarrow 2S = (1+1) + (1+1) + (1+1) + \dots \\ &\Rightarrow 2S = 1 + 1 + 1 + \dots \\ &\Rightarrow 2S=S \\ &\Rightarrow S = 0 \end{align}$$

Typically the extra conditions involve requiring all but a finite number of the terms to be $0$ ("almost all" in mathematical shorthand) or convergence conditions to make sure that the sum has a limiting value.

This question was asked on January 22, 2020, when I was in my senior year of high school. My questioning was very poor 😅. This is incomparable to someone like Peter Scholze who already known spectral sequences in high school 🙃。

0 人喜欢

Comments

There is no comment, let's add the first one.

弦圈热门内容

Base change map $U\times_{X}X\rightarrow U\times_{Y}Y$

My question: Let $X,Y$ be schemes. Let $X\rightarrow Y,X\rightarrow X, Y\rightarrow Y$ be morphisms of schemes. Why the morphism $U\times_{X}X\rightarrow U\times_{Y}Y$ is the base change of $X\rightarrow X\times_{Y}Y$ by $U\times_{Y}Y\rightarrow Y$?Here is the diagram I try, where the triangle is commutative. But I found that $(U\times_{Y}Y)\times_{Y}(X\times_{Y}Y)=U\times_{Y}X\times_{Y}Y=U\times_{Y}X$, i.e. I can not obtain the desired $U\times_{X}X$. What mistakes do I make?Here is the context ...

Power series expansion for sine function is Cauchy?

Consider the power series expansion of sine function $$S=(\sum_{i=0}^{j}\frac{(-1)^{i}}{(2i+1)!}r^{2i+1})_{i\in\mathbb{N}}, 0\leq r\leq2\pi.$$ Then is the series $S$ a Cauchy sequence?Let $\varepsilon>0$. Is it possible to find the very integer $N>0$ such that for any $m,n\geq N$$$\left|\sum_{j=n}^{m}\frac{(-1)^{j}}{(2j+1)!}r^{2j+1}\right|\leq\sum_{j=n}^{m}\frac{1}{(2j+1)!}r^{2j+1}<\varepsilon ?$$Proof 1. It is well-known that the power series expansion of $\sin x$ is convergent everywh ...

When is a scheme over an affine scheme affine?

Question: Let $X$ be a scheme. Let ${\rm{Spec}}(R)$ be an affine scheme for some ring $R$. Suppose that there is a morphism of schemes $f:X\rightarrow{\rm{Spec}}(R)$. What properties should $f$ have so that $X$ is also an affine scheme? Or what conditions can make $X$ affine?Answer: If $f$ is an affine morphism, then $X$ is affine by definition.This is an "if and only if". If $X$ is affine, the so is $f$. See theorem 7.3.7 in Vakil's Foundations of Algebraic Geometry, or 29.11.3 and 29.11.4 in t ...

Archimedean property written multiplicatively

My question: Let $(\Gamma,+,\leq)$ be an ordered abelian group. We know that archimedean property can be stated as: for all $a,b\in\Gamma$ with $a>0,b\geq0$, there exists $n\geq0$ such that $b\leq na$. However, if we consider the multiplicative case, namely $(\Gamma,\cdot,\leq)$ is the ordered abelian group. Is there exists Archimedean property written multiplicatively? I think there is. And I state that as follows: for all $a,b\in\Gamma$ with $b<1,a\leq1$, there exists $n\geq0$ such that ...

Is fully faithful functor between groupoids injective on objects?

My question: Let $\cal{C}$ and $\cal{D}$ be two groupoids, i.e. the category whose morphisms are isomorphisms. Let $F:\cal{C}\rightarrow\cal{D}$ be a fully faithful functor from $\cal{C}$ to $\cal{D}$. Then is $F$ injective on objects? In other words, is the object function $F:{\rm{Ob}}(\cal{C})\rightarrow{\rm{Ob}}(\cal{D})$ injective?Answer: No. Given any set $X$ we can construct a groupoid called the indiscrete groupoid on $X$, which has a unique (iso)morphism $x \to y$ for $x, y \in X$. Every ...

What do the local sections of an nilpotent ideal sheaf look like?

Question: Let $(X, O_X)$ be a scheme. and $I$ an nilptoent ideal sheaf. i.e. $I^n=0$ for some $n$. Would this imply that each $I(U)$ is an nilpotent ideal of $O_X(U)$?Answer: Let $I\subseteq \mathcal{O}_X$ be an ideal sheaf, and let $\mathcal{F}$ be the presheaf assigning to each open subset $U$ of $X$ the ideal $I(U)^n\subseteq \mathcal{O}_X(U)$. You say that $I$ is nilpotent of degree $n$ if $\mathcal{F}^\#$ is zero, where $\#$ is used to denote sheafification. But, since $\mathcal{F}$ is a se ...

A finite field extension of $\mathbb{R}$ is either $\mathbb{R}$ or isomorphic to $\mathbb{C}$

We need to prove the following proposition:Let $F$ be a field containing $\mathbb{R}$ with the property that $\dim_{\mathbb R}F < \infty$. Then either $F \cong \mathbb R$ or $F \cong \mathbb C$.We give three proof in the following, where the first one is the most simple, and the last one is the most complicated.Proof 1. By the uniqueness of the algebraic closure, we have an embedding $F \hookrightarrow \mathbb C$, hence we have $\mathbb R \subset F \subset \mathbb C$. The result follows from ...

Some thought of p-divisible groups and p-adic Hodge theory

The name "p-divisible group" is somewhat misleading, which in fact has another name "Barsotti-Tate group". A p-divisible group is not merely just a kind of group. lt is more general. In fact, a p-divisible group can be viewed as a tower of affine group schemes with some extra conditions. Historically, p-divisible groups were the main stimulus for p-adic Hodge theory. So l think that studying p-divisible groups is the key to study p-adic Hodge theory.However, today's p-adic Hodge theory is much m ...

Differences between collection, class, set, and family

A collection shall consists of mathematical objects that may not share some unambiguously properties. This is different from the so-called class, which consists of mathematical objects that share unambiguously properties. However, a class may not form a set. And we call such classes proper classes. What's more, a family is different from a class. A indexed family or simply family is a collection of mathematical objects that is indexed by a set called index set.--------------------This paragraph ...

One should do mathematics for the sake of oneself

Well, yesterday, when l was typing my articles excitedly, the boring class was over, so l had to stop this inspiring moment. What l wanna say at last is that one should really do mathematics for the sake of satisfying one's curiosity, You do mathematics maybe just to understand some kind of concepts. Our purpose of doing mathematics is not to have some specific problems solved, on the contrary, unsolved problems are the vitality of mathematics. Well, recently, l have written my essay named facto ...

cover

How to disable ESLint to some folders in NextJS app directory?

When executing npm run build in NextJS, eslint may check some folders that are unnecessary. If you are using App Router and want to disable ESLint to some folders, you can try the following ways.Edit next.config.jsYou can specify which directories should be checked by the ESLint. Here is the documentation: Linting Custom Directories and Filesmodule.exports = { eslint: { dirs: ['pages', 'utils'], // Only run ESLint on the 'pages' and 'utils' directories during production builds (next build) ...

cover

10 Things That Matter Most In Personal Finance

There are many factors that come into play when considering whether or not your personal finances are thriving or just barely surviving. Read on to learn what the top ten things that matter most in personal finance are, according to White Coat Investor.Today’s Classic is republished from White Coat Investor. You can see the original here.Enjoy!We spend a great deal of time on this blog discussing the minutiae of personal finance and investing. Examples include trying to decrease your portfolio e ...