高中数学对集合的定义就是根本性错误的！正是因为这个定义才导致了第三次数学危机的爆发，原因就是所谓的罗素悖论等等，假设存在一个集合的集合里面所有的元素都不属于它自身，然后矛盾！但是高中课本也完全没有任何说明，习惯性把它当作正确内容灌输给学生，因为确实在高中数学中所能遇到的集合确实都能构成集合。但是这却给我造成了困扰，我从高中开始就不止一次思考过，这个“集合"真的能构成集合吗？怎么样的“集合"才能构成一个集合？

直到大学，我因为学习代数几何的原因真正的深入接触集合论，才发现，这个定义其实是错误的，它其实应该是一个类的定义，不构成集合的类就叫做proper class。这些东西发展出来无非就是为了解决当时的种种悖论，其中一个很常见的就是所谓的ZFC公理系统。在ZFC公理下，所有的数学对象都能构成集合但是有的“集合”太大了，以至于它不能严格上称为一个数学对象，比如说所有集合的“集合”，所有R-模的“集合”，它们都构成一个类，而不是一个集合。但是如果它们小一点，ZFC公理规定了它们存在子集。

而为了避免所谓的proper classes，上个世纪60年代，Grothendieck提出了所谓的Grothendieck universes，它一种非空集合，在这个集合中，所有通常的集合运算都封闭，这看起来就像是个小“宇宙”。

高中数学有些内容严重脱节，没有顺应现代数品学的发展，也没有跟国际接轨。比如说函数其实就是集合间的一个对应关系，而映射有时候是函数的同义词，有时候意义更广。同时内容也误导同学对数学正确的理解。不过如果高中的时候，学校或老师多倡导同学多看数学书，而不仅仅是强调文学书，这个问题其实也能解决。

图1 旧高中教材对集合的定义

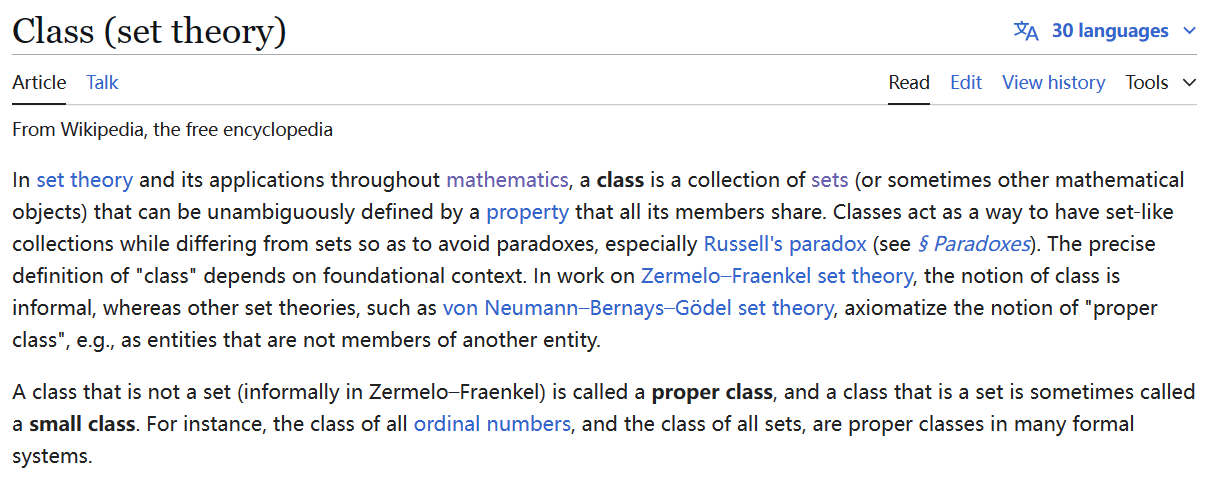图2 维基百科对类的定义

图3 Stack Project对类的定义

更新：

本文原先于2021年1月6号发布在我的QQ空间，上面三张图是现在重新再截一遍的，因为原先几年前的照片已经找不到了（帖子也被我删了，只剩下截图）。几年过去了，现在的高中教材也跟以前的不一样，我好不容易才找到以前高中数学教材对集合的定义。

现如今的高中教材，对集合的定义确实改进了，比原来的那个定义好多了，至少没那么误导性了。

图4 现在高中教材对集合的定义

这个新的定义对比维基百科上对集合的定义，意思上可以说也是非常接近。这个定义，虽不能说严格意义上的正确，但这对于高中数学这个阶段来说，已经完全够了，没必要引入那么复杂的集合论公理（本科也没有😄）。

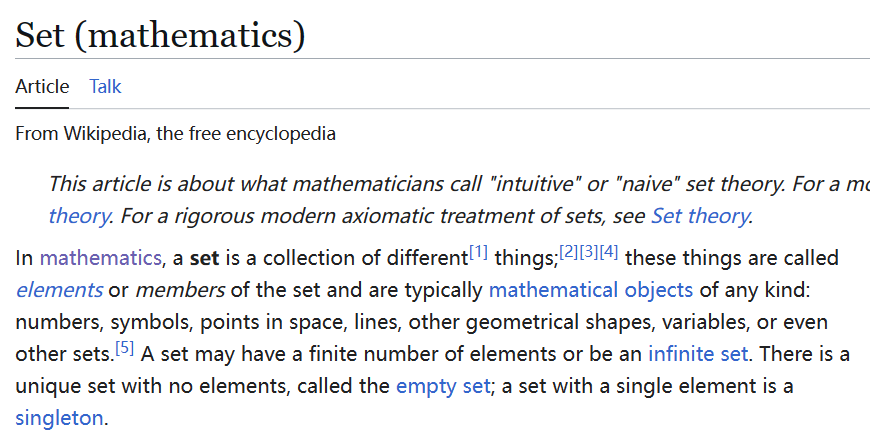图5 维基百科对集合的定义

看回自己以前说过的话，也不得不感慨世事变迁，那时候的我刚开始接触最前沿的数学，有些年少轻狂，也没有考虑大多数高中生对于数学的理解能力。旧的定义虽说是错的，但其实对于高中乃至本科阶段，影响其实并不是很大。